The Synergistic Power of Vector Embeddings & Cosine Similarity in AI-Driven Content Generation
How advanced AI technologies transform words into mathematical representations to create personalized content that matches your unique style
Introduction
Understanding the transformative role of AI in modern content creation
The proliferation of digital platforms has led to an unprecedented demand for content across various domains, ranging from marketing and journalism to research and entertainment. Artificial intelligence (AI) has emerged as a transformative force in addressing this demand, offering tools and techniques to automate and enhance content creation processes.
Among these advancements, the application of vector embeddings and cosine similarity stands out as a powerful paradigm for generating content that is not only semantically relevant but also capable of replicating specific writing styles and adapting to individual preferences.
Semantic Understanding
AI-powered content generation moves beyond keywords to understand the deeper meaning and context of language.
Style Replication
Advanced algorithms can analyze and mimic specific writing styles by understanding their mathematical representation.
Personalization
Content tailored to individual preferences through sophisticated vector-based similarity measurements.
Demystifying Vector Embeddings
How AI transforms words into mathematical representations
What Are Vector Embeddings?
At the core of AI's ability to understand and process human language lies the concept of vector embeddings. These embeddings serve as numerical representations of data points, encompassing words, sentences, and entire documents.
This conversion into a structured, numerical format is essential for machine learning models to effectively analyze and manipulate textual information. By mapping these data points into a high-dimensional space, vector embeddings capture the intricate meanings and relationships between them.
"The term 'vector' simply refers to an array of numbers with a defined dimensionality, while 'embeddings' denotes the specific technique of representing data in a way that preserves meaningful information and semantic connections."
How Vector Embeddings Work
- Words, phrases, or documents are converted into numerical vectors
- Similar concepts are positioned closer together in vector space
- These vectors typically have hundreds or thousands of dimensions
- Each dimension represents some aspect of meaning or context
- The proximity between vectors indicates semantic similarity
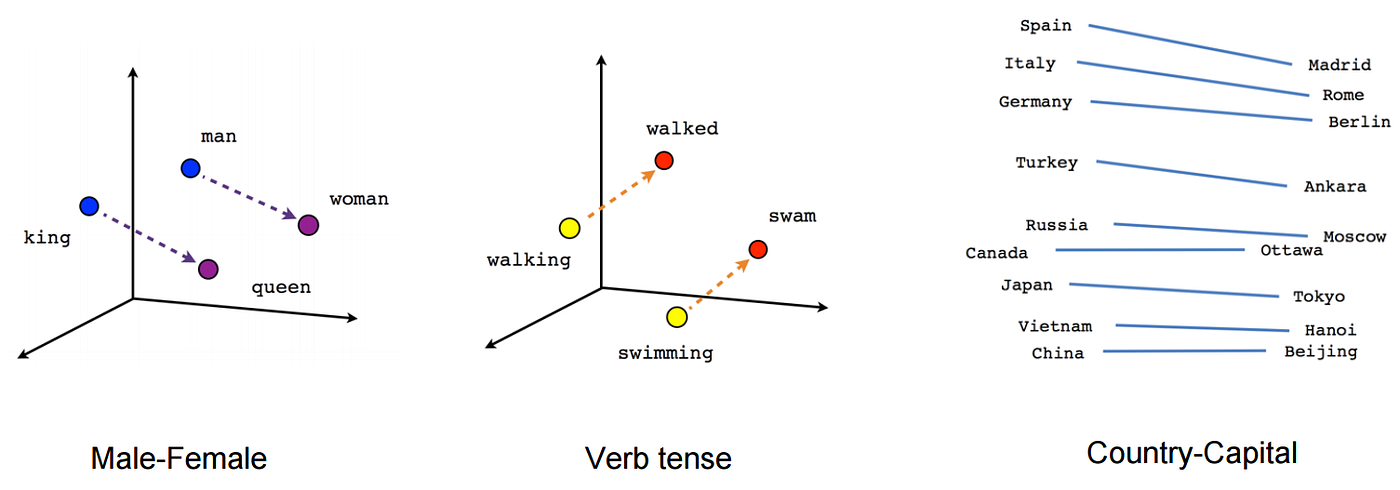
Visual representation of word embeddings in vector space
Creating Vector Embeddings
The creation of vector embeddings is achieved through machine learning processes where models undergo training on extensive datasets to convert various forms of data into numerical vectors.
Several techniques have been developed to learn these embeddings:
- Word2Vec: Learns word embeddings by analyzing word co-occurrence
- GloVe: Creates embeddings based on global word-word co-occurrence statistics
- FastText: Extends Word2Vec by including subword information
- BERT: Considers entire sentence structure for context-aware embeddings
- OpenAI Embeddings: State-of-the-art models like text-embedding-3-small
Applications of Vector Embeddings
Vector embeddings have found extensive applications across a wide spectrum of natural language processing tasks:
Sentiment Analysis
Determining emotional tone in text
Named Entity Recognition
Identifying entities in text
Text Classification
Categorizing text by content
Machine Translation
Converting between languages
Semantic Search
Finding meaning-based results
Style Mimicry
Replicating writing styles
Understanding Cosine Similarity
The mathematical foundation for comparing vector embeddings
What Is Cosine Similarity?
Cosine similarity is a fundamental metric used in data analysis to measure the similarity between two non-zero vectors that reside in an inner product space. It achieves this by calculating the cosine of the angle formed between the two vectors.
Mathematically, cosine similarity is defined as the ratio of the dot product of the two vectors to the product of their magnitudes (Euclidean norms).
Cosine Similarity Formula:
cos(θ) = (A·B) / (||A|| × ||B||)
Where A·B is the dot product of vectors A and B, and ||A|| and ||B|| are their magnitudes
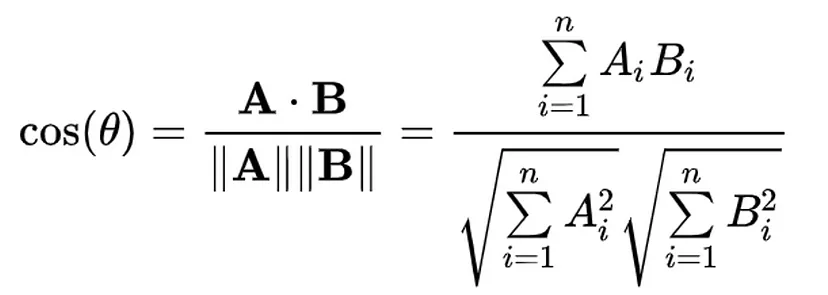
Interpreting Cosine Similarity Values
- 1.0: Identical vectors (0° angle)
- 0.0: Orthogonal vectors (90° angle)
- -1.0: Opposite vectors (180° angle)
- 0.7-1.0: High similarity
- 0.3-0.7: Moderate similarity
- 0.0-0.3: Low similarity
Why Cosine Similarity Excels for Text
Cosine similarity offers several advantages that make it particularly well-suited for text analysis and content generation:
- Focuses on the direction (angle) between vectors rather than their magnitude
- Effectively handles high-dimensional spaces common in text embeddings
- Performs well with sparse vectors where many dimensions are zero
- Ignores document length when comparing semantic content
- Computationally efficient compared to other similarity metrics
- Values are easily normalized to a range between -1 and 1
Applications in Content Generation
In the context of AI-driven content generation, cosine similarity serves several crucial functions:
Evaluating whether generated content aligns with a desired style or topic
Finding documents or passages with similar semantic meaning
Measuring style similarity between different texts
Guiding AI models to generate content with specific characteristics
Serving as a loss function when training neural networks
Implementing Cosine Similarity
/**
* Calculate cosine similarity between two embedding vectors
*
* @param array $vectorA First embedding vector
* @param array $vectorB Second embedding vector
* @return float Similarity score between 0 and 1
*/
public function calculateSimilarity(array $vectorA, array $vectorB)
{
// Ensure vectors have the same dimensions
if (count($vectorA) != count($vectorB)) {
throw new \InvalidArgumentException('Vectors must have the same dimensions');
}
// Calculate dot product
$dotProduct = 0;
$magnitudeA = 0;
$magnitudeB = 0;
for ($i = 0; $i < count($vectorA); $i++) {
$dotProduct += $vectorA[$i] * $vectorB[$i];
$magnitudeA += $vectorA[$i] * $vectorA[$i];
$magnitudeB += $vectorB[$i] * $vectorB[$i];
}
$magnitudeA = sqrt($magnitudeA);
$magnitudeB = sqrt($magnitudeB);
// Prevent division by zero
if ($magnitudeA == 0 || $magnitudeB == 0) {
return 0;
}
// Calculate cosine similarity
return $dotProduct / ($magnitudeA * $magnitudeB);
}Sample PHP implementation of the cosine similarity calculation used in our vector similarity system
Leveraging AI Models for Text Embeddings
A focus on OpenAI's text-embedding-3-small
State-of-the-Art Embedding Models
OpenAI has developed a suite of advanced embedding models, with text-embedding-3-small representing a significant step forward in terms of efficiency, performance, and cost-effectiveness compared to its predecessor, text-embedding-ada-002.
Designed for a wide range of natural language processing tasks, this model aims to provide high-quality embeddings that enable a deeper understanding of text. Alongside text-embedding-3-small, OpenAI also offers text-embedding-3-large, a more powerful model that generates embeddings with a higher dimensionality, catering to applications that demand even greater accuracy.
OpenAI Embedding Models Comparison
| Model Name | Dimensions | Max Input Tokens | MIRACL avg (%) | MTEB avg (%) | Price per 1M tokens ($) |
|---|---|---|---|---|---|
| text-embedding-3-large | 3072 | 8191 | 54.9 | 64.6 | 0.13 |
| text-embedding-ada-002 | 1536 | 8191 | 31.4 | 61.0 | 0.10 |
| text-embedding-3-small | 1536 (or 512) | 8191 | 44.0 | 62.3 | 0.02 |
MIRACL: Multi-language Information Retrieval benchmark; MTEB: Massive Text Embedding Benchmark
text-embedding-3-small Features
- Configurable dimensionality: Default 1536, can be reduced to 512 dimensions for better performance
- Long context support: Processes up to 8191 tokens in a single request
- Matryoshka Representation Learning: Maintains performance even at reduced dimensions
- Normalized vectors: Simplifies cosine similarity calculation to a dot product
- Improved performance: Better results on benchmark datasets than previous models
- Cost-effective: 80% lower cost than text-embedding-ada-002
Application to Style Mimicry
The enhanced capabilities of text-embedding-3-small make it particularly valuable for style replication and personalization:
Encoding Stylistic Elements
The model can capture subtle patterns in vocabulary, sentence structure, and tone that define a writer's unique style.
Comparing Writing Samples
Using cosine similarity, we can quantify how closely a generated piece matches the style of reference samples.
Style-Based Content Personalization
User-provided writing samples can be converted to embeddings and used to guide content generation matching their style.
Content Recommendation
Finding content that matches a user's stylistic preferences based on similarity between their writing embeddings and content embeddings.
The Strategic Importance of Consistent Writing Style
Why vector-based style analysis delivers business value
Maintaining a consistent writing style across all communication channels is of paramount importance for effective branding, clear communication, and enhanced audience engagement. Our vector similarity technology makes this possible at scale.
Branding Benefits
- Increases brand recognition and awareness
- Builds trust and credibility with customers
- Reinforces brand personality and values
- Differentiates from competitors
- Increases customer loyalty and retention
- Boosts brand worth and revenue
Communication Benefits
- Enhances clarity and comprehension
- Builds trust and professionalism
- Reduces misunderstandings
- Creates reliable information flow
- Improves communication efficiency
- Contributes to professional appearance
Engagement Benefits
- Makes content more relatable
- Creates a consistent experience
- Builds stronger audience connections
- Establishes a recognizable voice
- Increases audience loyalty and trust
- Improves content reception
Experience the Power of AI-Driven Style Personalization
Our vector similarity system allows you to maintain consistent brand voice while personalizing content to match your unique style. See how our technology can transform your content creation process.